로또 및 큰 수의 법칙간 상관관계에 대해 이야기를 해볼까 합니다.
▶ 큰 수의 법칙이 무엇인가요?
통계학에서 사용되는 평균과 관련된 개념입니다.
▶ 로또와 해당 법칙과는 무슨 관계가 있나요?
아무 관계가 없음에도 해당 법칙을 로또에 적용하려 하는 사람들이 일부 존재합니다.
해당 글은 주제와 관련된 이론을 토대로 본인의 주장을 서술한 글이며 일반적인 의견과는 크게 다를 수 있습니다.

로또 및 큰 수의 법칙간 상관관계
심심하면 한번씩 언급되는 로또는 약 20여년간 1등 배출을 하면서 수만명에게 일확천금의 기회를 주게 되었습니다. 하지만 1등이라 해도 파이 나눠먹기 방식의 복권인 탓에 매회차 당첨금이 일정하지 않아 최악의 경우 아파트 1채도 제대로 구매하지 못하는 금액을 받은 사례도 있습니다.
로또를 이야기하다보면 무조건 등장하는 것이 있습니다. 연구가 가능하다는 사람들과 그렇지 않은 사람들인데 다수의 사람들은 독립시행을 근거로 들며 로또는 연구가 불가능하다라고 주장하고 있습니다. 실제로 그 어떠한 가설을 가져다놓아도 사실상 무적의 논리인 독립시행을 이길 수 있는 것은 존재하지 않습니다. 이 글에서 이야기 하는 큰 수의 법칙 역시 독립시행을 이기는 것은 불가능하지만 해당 내용에 대해 잠깐 짚고 넘어가보려고 합니다.
큰 수의 법칙이란?
큰 수의 법칙은 통계학에서 다루는 가설이 아닌 증명된 이론 중 하나로서 일정한 크기의 표본을 조사할때 표본 평균이 모집단의 평균에 근접해질 가능성이 높아진다는 이론입니다. 이미 수학적 증명을 통해 입증되었으며 저는 수포자이므로 정확한 내용이 궁금한 사람들은 다른 정보를 찾아보는 것을 추천드립니다.
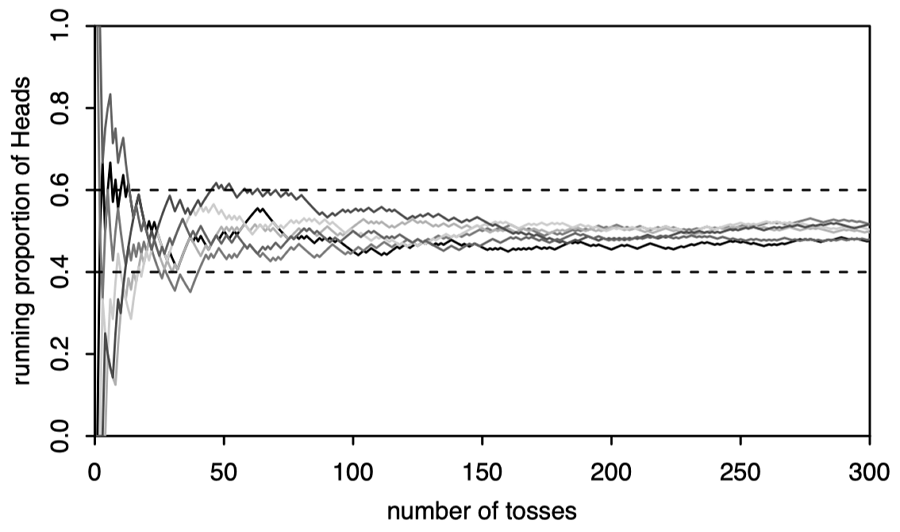
큰 수의 법칙을 로또에 적용시키려는 사람들
대한민국에서 로또 1등 확률은 약 814만분의 1이며 퍼센트 확률로 따지면 0.0000123% 정도입니다. 당첨된다라는게 사실상 불가능한 확률이지만 아예 하지 않으면 0%이며 한장이라도 구매할 경우 확률이 아주 미세하지만 늘어나기 때문에 당첨확률을 높이려면 최소한 로또를 한장 더 사는 것 외에는 더 좋은 방법은 존재하지 않습니다. 대부분 로또를 한번 살때 5천원어치를 구매하면 실제 본인이 당첨될 확률은 814만분의 5가 될테니까요.
그런데 로또를 큰 수의 법칙에 적용시키려는 사람들이 있습니다. 회차를 늘려갈 수록 번호가 균등하게 분포되기 때문에 이를 토대로 연구를 하는 사람들이 있습니다. 예를들면 나오지 않은 수를 토대로 번호를 뽑든가 그 반대로 많이 나온 수를 뽑는 행위를 말입니다.

// 그런데 그것이 실제로 일어났습니다 //
문제는 로또 1019회에서 발생했는데요 1등 당첨자수가 무려 50명이 나온 것입니다. 당첨자수는 역대최고이며 반대로 당첨액수는 역대 두번째로 최저인 4억 4천만원이라고 하는데 세금을 제외하면 3억원대로 더 낮아지게 됩니다. 여기서 나온 로또 번호가 바로 현재까지 뽑은 로또 번호 중 많이 나온 번호를 조합하여 나온 번호이기 때문입니다.
물론 이것은 독립시행에 의한 운적인 요소에 불과한데도 여러가지 이유를 들어 로또가 연구가 가능하다는 사람이 있으며 큰 수의 법칙 역시 흔하게 등장하는 이론 중 하나입니다. 둘을 완전 다르게 놓고 봐야 하는데도 동일선상에 놓게 되므로서 발생하는 오류 중 하나입니다.

로또가 연구가 가능하다는 사람들의 주장 중 몇가지
1. 큰 수의 법칙은 증명된 이론이다.
2. 로또는 확률이 0이 아니며 적지만 존재한다.
3. 로또 확률만큼 시행을 하게 되면 로또번호가 현재와 같이 들쑥날쑥하지 않을 것이다.
4. 하지만 로또는 무한히 시행하지 못한다.
5. 현재까지의 데이터는 유의미하다.
6. 1등이 아니더라도 이하 등수에 대한 연구는 가능하다.
대략 이런식인데요 일부 주장하는 사람들 가운데서는 무한히 시행을 할 수 없다는 이유를 들어 연구가 가능하다는 사람들도 있습니다. 예를들면 우리가 앞으로 살날을 최대 100년이라 가정했을대 현재 기준 100년동안 로또를 추첨해도 5200회밖에 추가하지 못합니다. 즉 죽을때까지 돌려도 현재 회차에서 7000회도 가지 못한다는 뜻이기도 합니다. 무한히 시행할 수 없는 조건에서 무한을 따진다는게 어찌보면 앞뒤가 맞지 않는 일일지도 모르겠지만...어쨌든 이러한 주장을 하는 사람들도 있습니다.
또한 큰 수의 법칙은 말 그대로 무한히 시행했을때 얻을 수 있는 결과를 이론으로 나타낸 것이기 때문에 무한히 시행할 수 없는 조건이라면 1등이 아니더라도 최소 3~4등정도되는 일정부분 연구는 가능할 것이다라는 주장을 하는 사람들도 일부 존재합니다. 어떠한 주장을 하더라도 독립시행을 이길 수 있는 주장은 존재하지 않긴 하지만 이런걸 듣고 있으면 저도 모르게 혹하게 되는 순간이 종종 있긴 합니다.
로또 및 큰 수의 법칙간 상관관계에 대해 이야기를 해보았습니다. 이론이 적용된다 하여 그 이론이 독립시행에도 연관성이 존재하는 것은 아닙니다.
'생활정보' 카테고리의 다른 글
| 샤워할때(목욕할때) 핸드폰(휴대폰) 들고 들어가는 사람 (0) | 2023.04.18 |
|---|---|
| 1분기(1/4)분기 2분기(2/4)분기 3분기(3/4)분기 4분기(4/4)분기 반기 뜻 의미 (0) | 2023.03.27 |
| 다니던 학원 그만둘때(옮길때) 문자 전화 카톡 어떠한 멘트를 쳐야 할까 (0) | 2023.02.06 |
| GS CU편의점 택배 주말(토요일 일요일) 접수 및 수거 여부 (0) | 2023.01.26 |
| 지겨운 회식 빠지는법 적절한 불참 사유(핑계) 무엇 (1) | 2023.01.12 |




